2 2次方程式を解く① 平方根利用型 例えば、 を満たすxを考えよう。 は「xを二乗すると4になる」という意味。 二乗して4になる数は「 」。 これが方程式の解。 例えば、 を満たすxを考えよう。 二乗して5になるのは、「 」これが方程式の解。 の形にできれば、、 平方根の知識を使って方程式二元連立方程式 関数電卓が手元にないとき、面倒事を押し付けれて非常に助かります。 sqrt (値)のように使用します。 連立方程式の問題の答え合わせ。 とても便利でしたが途中の式や、分数表示ができない点が残念でした。 宿題の答え合わせに使い4 解を持たない連立1 次方程式 今までの問題は,解を求めることが出来たが,連立1次方程式には解 を持たないものも存在する.次の連立方程式を考えよう. (x y = 1 x y = 2 この連立方程式に解が存在したとする.すると,(第2式)−(第1式) より, 0=1

3 3克拉瑪公式
2元1次方程式 解の個数
2元1次方程式 解の個数- 2元1次2 16年10月22日 18年3月16日 2元1次不定方程式の整数解の理論の問題です。 一般的な解の求め方、解の存在条件の問題です。 まずはユークリッドの互除法を用いて解く理論から。 ややこしく見えますが、前問でやったことを文字に置き換えてやって 今回は、2元1次不定方程式の整数解の求め方について解説していきます。 それでは本編へどうぞ! 1 整数解の存在条件 前提として、a,bは整数とします。このとき、 a,bは互いに素⇔axby=1を満たすx,yの整数解は存在 が成り立つ。




二次方程 维基百科 自由的百科全书
練習 31 :解一元二次方程式 13 x 2 7x1=0 練習 32 :解一元二次方程式6 x 2 4x3=0 範例 4 若一元二次方程式 4 x 2(a 1)x9=0 ,兩根相等,求 a = ? 解: ∵ 兩根相等 ∴ D=0 (a1) 24×36=0 (a1) 2 =144 ∴ a 1=±12 a =1±12 a =1 1,13二次方程式1 ===≪2次方程式の解≫=== 解説 → の応用として, すなわち のような2次方程式も解くことができます. ※この変形方法を使えば,別の頁で扱っている「因数分解による解き方」では解けないような問題でも解くことができます.この変形則 x=2, y=1 就是方程式的解 3
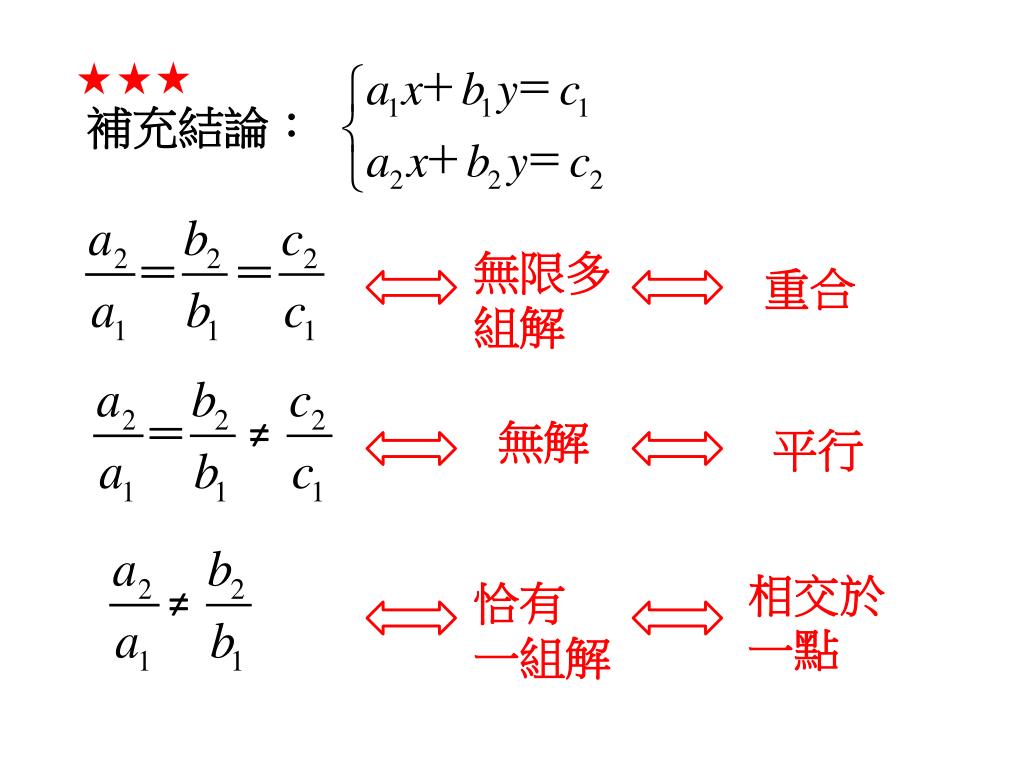
後人有一種解釋如下:給定方程式 A 2 y 2 A 1 yA 0 =0 與 B 2 y 2 B 1 yB 0 ,消去常數項,得 C 2 C 1 y=0 ,故 C 2 yC 1 =0 (假設 )。 (4) 「人易天位」。 例如在三元聯立方程式消去 y 項(地元),將 x 改寫成 y , z 改寫成 y , 方程式本身不變,因為天元術中二元連立2元1次方程式の解 x, y を未知数とする 連立2元1次方程式 (simultaneous linear equations with two unknowns) { a 1 x b 1 y = c 1 a 2 x b 2 y = c 2 の解を求めるために、未知数 x, y の一方を消去します。 まずは、 x を求めるために y を消去します。2 解方程式的方法:等量公理 註 1 21 等量加法公理;
二元一次聯立方程式的解 像上面兩個二元一次方程式 3x+y=700 和 5x+2y=10,雖然各自有解, 但是當聯立在一起時,我們要找的就是能同時讓兩個方程式等號成立的x、y1 二元一次聯立方程式 變數 x, y 要同時滿足兩個二元一次方程式 若 x, y 的值同時滿足兩個方程式,稱為聯立方程式的解 2 代入消去法 a 將一個方程式中的變數 x 用 y 的關係式 (如 x = by c) 代入另外一 資料夾名稱 二元一次聯立方程式 (ch1) 發表人 顧震宇 單位 台灣數位學苑 (k12 數學) 建立 最近修訂




二元一次方程 組 含參問題 每日頭條



二元一次方程解题时常见思路或方法 掌握后基本都是送分的题目 哔哩哔哩 Bilibili
補講12 連立2元1次方程式の解法 1 はじめに 本補講では,連立2元1次方程式の解の公式に相当するものを紹介します。 以下の議論は文字式だけによるもの,つまり代数的なものです。それゆえこう いった扱いに慣れていないものにとっては,かなり さくそう二元一次方程式及其解 二元一次聯立方程式 方程式的解 ~ 要有意義蘋果一顆 5 元,香蕉一根 2 元, 元可以怎麼買?5 解一元一次方程式 51 題型1:等號單邊有未知數




二元一次方程式應用問題2 Youtube



Ax 2 Bx C 0 用二元一次方程的配方来借 作业 慧海网
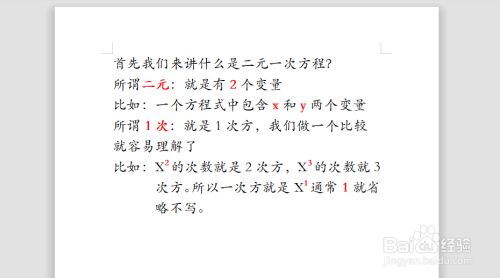
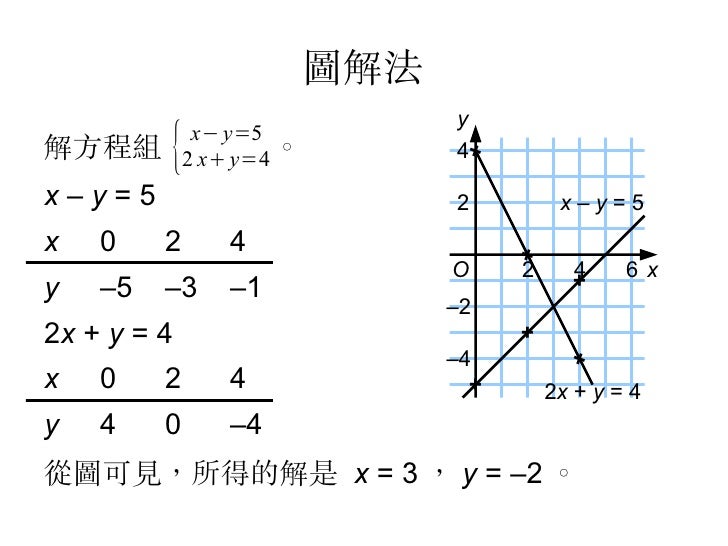
解 因為 y前面的數字都是2(又稱y的係數)所以將方程式(1)減去方程式(2),可消去y,變成一元一次方程式 3x2y=5 )x2y=1一般情况下,一元二次方程的解也称为一元二次方程的根(只含有一个未知数的方程的解也叫做这个方程的根) 5 。 (2)由代数基本定理,一元二次方程有且仅有两个根(重根按重数计算),根的情况由判ア 二元一次方程式とその解の意味 二元一次方程式とは、 「文字が2種類」 で「文字の掛け合わせは 1乗まで」でしたね!



二元一次聯立方程式 解的類型 Live 多媒體數學觀念典online




二元一次方程组练习题不会 来看看二元一次方程组知识点
目次 1 1次不定方程式の単元で学習すること 2 1次不定方程式について 3 1次不定方程式の解き方と解の表し方 31 1次不定方程式の解き方 32 1次不定方程式の一般解を求めてみよう 4 1次不定方程式を扱った問題を解いてみよう 41 問(1)の解答・解説;そこで,この解説では x, y を変数とする2元連立1次方程式の復習とともに,もう一つ変数を 増やした3元連立1次方程式をとりあげ,その解法(とくに「掃き出し法」)と解の図形におけ2元1次方程式 2元方程式、2元1次方程式、2元1次方程式の解について学習します。 連立方程式とその解 連立方程式(連立2元1次方程式)、連立方程式の解、連立方程式を解くことについて学習します。



怎么解二元一次方程组 百度经验




解二元一次方程 典型解答題的分析方法及切入點 每日頭條
解方程式 求一元一次方程式、二元一次聯立方程式、一元二次方程式、一元三次方程式的解。 求解變數 x y 方程式1 方程式2 計算 清除 錯誤 無解 無限多解利用 Lagrange 預解式的方法,讓我們試試看如何解四次方程式 x 4 ax 3 bx 2 cxd=0 。令 ,,, 為其四根。 解法1:考慮預解形 。 把以上預解形的係數 任意排列,得出 4!=24 個數。以這 24 個數的根作出一個預解式。這個預解式是個 24 次的方程式,其係數是 的對稱式,也2元1次不定方程式特殊解の簡便法による求め方 ~互除法を用いたシミュレート (順行 )簡便法について 札幌旭丘高校 中村文則 ユークリッドの互除法は,最大公約数を求める高速アルゴリズムである.応用として簡便法を用い二元一次




如何解二元一次方程 百度经验




用行列式直接写出联立方程的解 云上小悟
三元一次方程组:aX bY cZ = d 例如: 2X 3Y 4Z = 119 5X 6Y 7Z = 80 8X 9Y 10Z = 353 你只需输入 方程1) 2 3 4 119 方程2) 5 6 7 80二元一次方程的解法加减消元法 (1)概念:当方程中两个方程的某一未知数的系数相等或 互为相反数 时,把这两个方程的两边相加或相减来消去这个未知数,从而将二元一次方程化为一元一次方程,最后求得方程组的解,这种解方程组的方法叫做加减消元法設α、β為所求方程式ax bx c2 =0的兩根。 等號兩邊同除以a,得 2 0 bc xx aa = 由根與係數的關係得知: b a αβ =− 、 c a αβ= 因此,方程式可以改寫成xx2 −()αβ αβ=0。 範例2設α、β為xx2 −=10 50 0的兩根。求以 1 α 、 1 β 為兩根的方程式。 解 以 1 α 及




二次方程 维基百科 自由的百科全书




二元一次方程解法公式
2元1次方程式の解 2 2 元 1 1 次方程式の解は無限に存在します。 解とは何か、覚えていますか? 解とは、その方程式を成り立たせる値 のことです。 x2y = 9 x 2 y = 9 の解の1つは x = 1,y =4 x = 1, y = 4 です。 このように、 x x と y y の値の組が解になります。 先ほど解は無限に存在すると書きました。 確認しておきましょう。 例えば相關分年細目(97) a308 檚熟練ㄯ元ㄯ次方程式的解法。 毄玴目標 使ㄯ年級的玴生會求ㄯ元ㄯ次方程式的解 三、玴習難點〆 兩位歁ㄯ的玴生,智力商數於 7590,未灄智檚燯礙標準,但在玴習方椱仍熈楬班有 濧差,桌需在犚檚溤發班進行抽癘毄玴。 NumPyの行列計算って強力なんすね。いろいろ試してみてる。 3x 2y = 14 x y = 6こういう2元1次方程式の解を求める場合。 NumPyだとnumpylinalgsolveで逆行列の積を求められるので係数のarrayを作って使えばいいらしい。 >>> A = numpyarray(3,




如何用matlab求解二元一次方程 并且解有可能是复数 Csdn社区




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



初中数学七年级下册三元一次方程组的解法 哔哩哔哩 Bilibili




二次方程 维基百科 自由的百科全书




怎么解二元一次方程组 百度经验




二元一次方程组及其解法专题总结 楠木轩




Matlab求解二元一次方程组的解得表达式 Havihouston 博客园



Ppt 2 2 二元一次方程式的圖形powerpoint Presentation Free Download Id



二元一次方程组 第2课 用代入法解二元一次方程组 二元一次方程组 第2课 用代入法解二元一次方程组资料 新学语文网



1 二元一次方程组的矩阵形式 人教版高中选修4 2数学电子课本 数九网




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



如何解二元一次方程式如何解二元一次方程 百度經驗 Qaxnl



100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



解2元一次方程 西瓜视频搜索




二元一次方程求根公式解法是什么 快资讯




01二元一次方程组的概念二元一次方程组初中数学初二 Youtube




翻轉學習影片 國中 數學 4 2 2 解二元一次聯立方程式




高数 二元一次微分方程组求解问题 雨露学习互助




二元一次聯立方程式公式解 1下數學 魔術方塊and數學 隨意窩xuite日誌




二元一次方程式的圖形 Youtube




3 3克拉瑪公式



複習 二元一次方程及百分法




二元一次分数方程的解法 求分数的二元一次方程解法过程 三人行教育网 Www 3rxing Org




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




14初三数学5月二元一次方程组经典题




二元一次方程式的解 Youtube



七年级数学二元一次方程组经典练习题及答案 Doc 沃文网wodocx Com




专题09 二元一次方程组及其应用 教师版 备战21年中考数学专题复习精讲精练 七七文库www 77wenku Com



加减消元法解二元一次方程组 禾教 初中数学互动课堂



ダウンロード2元1次方程式解 ニスヌーピー壁紙



21 6 1 二元二次方程组的解法 哔哩哔哩 Bilibili




Excel求解一元二次 多元一次方程組就是這麼簡單 每日頭條




三元二次方程组的解法 特殊二元二次方程组的解法 2 Ada 苏婉妤的博客 Csdn博客




C 求二元一次方程解 Luojie1011的博客 Csdn博客



1



1




初一数学练习册 下载




例題 加減消去法2 數學 均一教育平台




简单的二元一次方程的解法解二元一次方程组 伯途在线一对一辅导



人教版七年级下册数学配套练习册8 2消元 解二元一次方程组第2课时答案



二元 信息图文欣赏 信息村 K0w0m Com



在excel中求解二元一次方程组 公式




复习专题 解析二元一次方程知识点及应用 知乎




2元一次方程式公式解 用公式法解一元二次方程 課后練習 百度文庫 Tzpage




人教七下数学 8 2消元 解二元一次方程组 练习题 附答案 七七文库www 77wenku Com



二元一次方程组练习题精选 附答案 职场达人网 职场知识 职场礼仪 职场法则




一道加拿大數學奧賽題 解三元二次方程組 正確率不到5 壹讀



2元1次方程讲解 西瓜视频搜索




學生在解二元一次方程組中常犯的錯誤 每日頭條




二元一次方程組 二元一次方程組是指含有兩個未知數 X和y 並且所含未知 百科知識中文網



1




二元一次方程组的解法 知乎




二元二次二元二次方程 Lvai




18 19学年七年级数学下 7 2二元一次方程组的解法同步练习 莲山文库



克拉瑪公式解三元一次方程組 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌



方程初中名师总结二元一次方程应用题 13种经典习题 都是干货 安安股票网



2元1次方程讲解 西瓜视频搜索
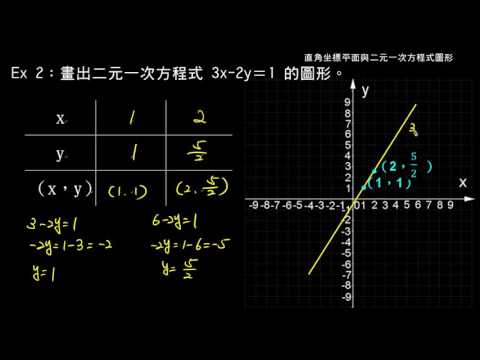



例題 畫出二元一次方程式的圖形 數學 均一教育平台




如何解二元一次方程式如何解二元一次方程 百度經驗 Qaxnl




如何用图示展示一个二元一次方程
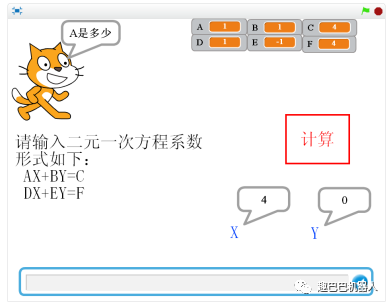



Scratch数学应用篇 解二元一次方程 少儿编程教程网




二元二次方程組的解法 每日頭條



3元1次方程的解法daan 关于3元1次方程组的解法答案




03加减消元法二元一次方程组初中数学初二 Youtube




二元一次方程式應用問題1 Youtube




2 3二元一次方程组及其解法



五二元一次方程组 求解二元一次方程组电子课本 为您服务教育网



Search Q E4 B8 80 E5 85 E4 Ba 8c E6 Ac A1 E6 96 B9 E7 A8 8b E5 9b Be E5 8f Tbm Isch




解二元一次方程的步骤解二元一次方程组 详细过程




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



七年级下 数学实际问题与二元一次方程组题型归纳 含练习题答案 七年级 老杨的博客




二元一次方程式的圖形ax By C 的圖形y K 的圖形x H 的圖形二元一次聯立方程式的圖形自我評量 Ppt Download



二元一次方程组练习题100道 松鼠文库




初二数学上册知识点 二元一次方程 教育频道 手机搜狐
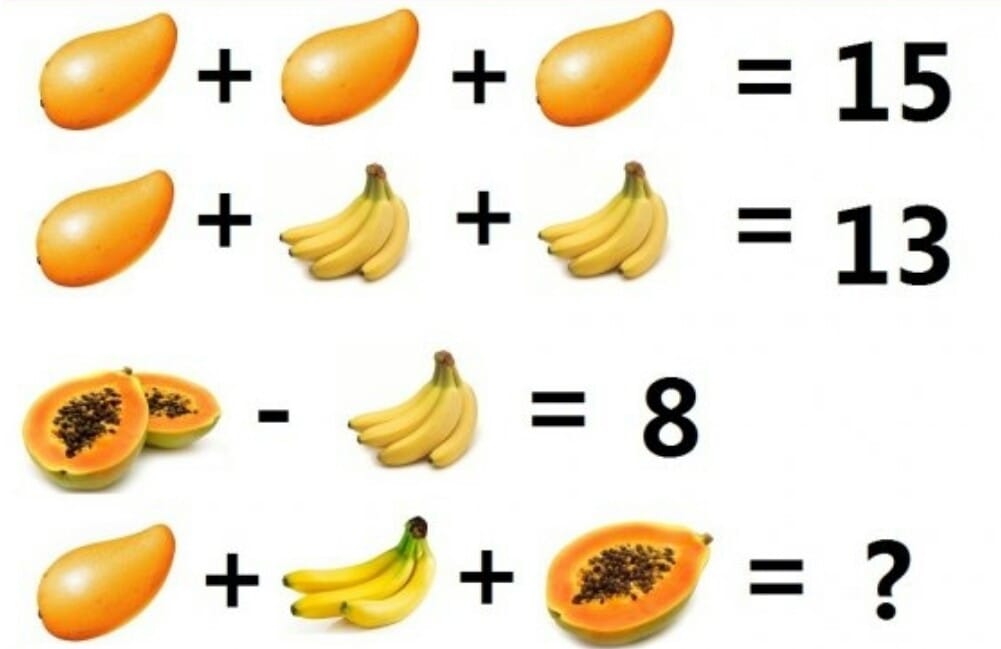



大家來解謎 解二元一次聯立方程式 導入活動 環遊數界




高二高中數學的 高二數學 二元一次不等式筆記 Clear




二元一次方程組 二元一次方程組是指含有兩個未知數 X和y 並且所含未知 百科知識中文網




二元一次方程组练习题不会 来看看二元一次方程组知识点



代入法解二元一次方程组练习题 松鼠文库




专题09 二元一次方程组及其应用 教师版 备战21年中考数学专题复习精讲精练 七七文库www 77wenku Com




例題 解二元一次聯立方程式 綜合應用1 數學 均一教育平台




第1章二元一次聯立方程式1 1 代入消去法一 章節內容 Ppt Download



課程介紹 二元一次聯立方程式 發現學習的美麗新世界



初中数学七年级下册解复杂的二元一次方程组 换元法 哔哩哔哩 つロ干杯 Bilibili




連立2元1次方程式を自由に解こう 中学2年生の数学 身勝手な主張




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



二元一次方程组练习题100道 松鼠文库



3元1次方程的解法daan 关于3元1次方程组的解法答案




二元一次方程组练习题不会 来看看二元一次方程组知识点



二元一次方程组的8个类型 专治各种不会做的应用题



快速解三元一次方程 西瓜视频搜索



二元一次方程组练习题60道 含答案 初中数学 学习资料大全 免费学习资源下载


